planimetria ICSP: W okręgu o środku O poprowadzono cięciwę AB. Miara kąta zawartego między cięciwa AB a styczną do okręgu poprowadzoną w punkcie B wynosi 58^◯. Wyznacz miary kątów trójkąta AOB.

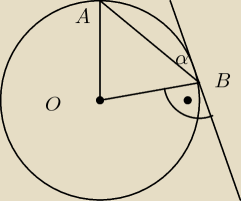
Trivial: α = 58^o

Trivial: I zauważ, że AO = OB = r.

ICSP: A no tak styczna jest pod kątem prostym do punktu styczności...

	π
W okręgu o promieniu 3cm cięciwa AB wyznacza łuk o długości		. Wyznacz miarę kąta
	2

zawartego między cięciwa Ab a styczną do okręgu w punkcie A.

Trivial:

	π
Trzeba obliczyć jaki kąt tworzy łuk o długości		w okręgu o promieniu r = 3 cm.
	2

Trivial: Potem to już proste

ICSP: czyli chodzi o to:

	l
α =
	r

	π
α =		= 30 stopni
	6

Trivial: Tak.

Trivial: Potem liczysz kąty przy podstawie (równoramienny) α + 2β = 180^o

	180o − α
β =
	2

Dalej: γ − kąt o który pytają w zadaniu γ + β = 90^o

	α		α
γ = 90o − 90o +		=		.
	2		2

ICSP: 15 stopni wychodzi

Trivial: Chyba tak... Masz odpowiedzi do tego?

ICSP: Mam ale nie zaglądam bo zaraz od razu spojrzę na następne. Sprawdzam po 10 zadań.

Trivial:

Trivial: To dawaj następne.

ICSP:

	n−2
Już ostatnie(na razie Wykaz że kąty wewnętrzne n−kąta foremnego mają miarę		* 180
	n

stopni.

Trivial: Suma kątów wewnętrznych w n−kącie to: (n−2)*180^o Czyli w foremnym n−kącie, gdzie wszystkie kąty są równe miara jednego kąta to:

(n−2)*180o
n

A jak wykazać to pierwsze, to nie wiem jeszcze.

ICSP: ok. Dzięki za wszystkie poprzednie

Trivial: Każdy n−kąt można podzielić przekątnymi na (n−2) trójkątów (odpowiednio), a suma kątów w każdym z nich to 180^o. Jedyne co przychodzi m na myśl, to właśnie to.

Trivial: Sprawdź w odpowiedziach, czy dobrze.

ICSP: Właśnie nie mam odpowiedzi do wykazywania. Mam same wyniki podane.

Trivial: Z jakiej książki robisz, tak z ciekawości...?

ICSP: MATeMAtyka. Podręcznik dla III klasy liceum zakres rozszerzony zad strona 228.

Trivial: A wydawnictwo?

ICSP: nowa era. Po zrobieniu tych zadań z cięciwami od razu ruszyłem do przodu. Już 3 zadanka poszły bez twojej pomocy

Trivial: No widzisz.

ICSP: a coś takiego? Obwód rombu jest równy 20 a suma długości jego przekątnych wynosi 12. Oblicz pole i wysokość tego rombu. 4a = 20 a= 5 d₁ + d₂ = 12

	d1		d2
(		)2 + (		)2 = 25 Dobry jest to układ równań Chyba zły bo mi złe wyniki
	2		2

wychodzą.

Trivial:

	d1d2
P =
	2

nora: Jeśli potrzebujesz wyprowadzenie niegeometryczne to tak: α=360⁰ zakładasz że trójkąt ABC jest równoramienny wtedy:

	3600
<ABC =<ACB=(1800−α):2=(1800 −		):2
	n

zatem kąt wewn. jest równy 2*<ABC

	3600
2*<ABC = 2*(1800−		):2
	n

	360		180n−3600		1800(n−2)
1800 −		=		=
	n		n		n

ICSP: Znam wzór na pole ale mam sumę nie iloczyn.

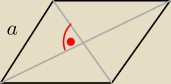
Trivial: Układ dobry.

ICSP: no jasne √54 = 2√14 a nie tka jak ja genialny liczyłem 2√19...

Trivial: Teraz pole z przekątnych i ze wzoru P = ah i porównujesz.

ICSP: Zrobiłem Znowu dziękuję za pomoc.

Trivial: Można zrobić tak:

⎧	d1 + d2 = 12 /2
⎩	(d1/2)2 + (d2/2)2 = 25 /*4

⎧	d12 + d22 + 2d1d2 = 144
⎩	d12 + d22 = 100

2d₁d₂ = 44

	d1d2
P =		= 11.
	2

ICSP: Idziemy z kolejnym. Przekątne równoległoboku mają długości 8 i 16 a kąt zawarty między nimi ma miarę 60 stopni. Oblicz obwód tego rombu.

ICSP: Tego równoległoboku oczywiście.

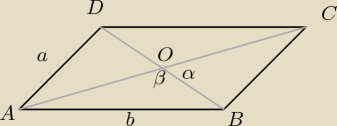
Trivial: d − krótsza przekątna D − dłuższa przekątna ΔBOC (tw. cosinusów):

	d		D		d		D
a2 = (		)2 + (		)2 − 2*		*		cosα
	2		2		2		2

a = ... ΔAOB (tw. cosinusów): β = 180^o − α

	d		D		d		D
b2 = (		)2 + (		)2 − 2*		*		cosβ
	2		2		2		2

L = 2(a+b) = ...

ICSP: Już widzę podstawę stosującą twierdzenie cosinusów kąt DBC nie jest prosty?

Trivial: Czemu nie... Ja chyba zastosowałem tw. cosinusów na podstawie, bo nie chciało mi się myśleć. Ogólnie to jestem taki sobie z geometrii. A czy kąt DBC jest prosty to nie wiem.

ICSP: To może ktoś się skusi na kolejne? W trapez równoramienny wpisano okrąg. Oblicz pole i obwód tego trapezu jeśli tego kąt ostry ma miare 60 stopni a promień okręgu opisanego na tym trapezie jest równy 1

Zimny: masz odpowiedz? mi wyszlo:

	16√3
Ob:
	3

	8√3
P:
	3

ICSP: Odpowiedzi są inne.

Zimny: 1sek, znalazlem blad

Zimny: ob=8√3?

ICSP: również pudło.

Zimny: to odpadam , wracam do swoich obowiazkow

ICSP: Pomoże ktoś. Mi sie już pomysły skończyły:(

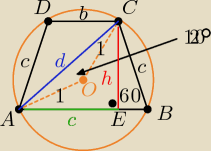
Eta: Z warunku wpisania okręgu w trapez

	a+b
a+b= 2c =>		= c
	2

	a+b
P=		*h = c*h
	2

	h
		= sin60o
	c

	c√3
h=
	2

	c2√3
P=		i Ob= 4c
	2

z tw. cosinusów w trójkącie AOC d²= R²+r²−2R²*cos 120^o => d²= 3

	a−b
|EB|=
	2

to:

	a+b
|AC|=		= c
	2

z tw. Pitagorasa w ΔAEC h²+c² = d² 7c²= 12 => c²= ¹²₇ i teraz dokończ ......... odp:

	6√3
P=		[ j2]
	7

	8√21
Ob=		[ j ]
	7

Eta: Godzio ......... zerknij , bo o tej porze mogłam się pomylić w rachunkach

Eta: oczywiście chochlik: d²= R²+ R² −2R²*cos120^o

Eta: No dobra, to idę do spania Dobranoc ...... Godzio

ol: skad wynika, ze kat AOC ma 120 stopni...?

ICSP: kąty wpisane i opisane na tym samym łuku.

Tomas: W okręgu o promieniu 6 cm poprowadzono cięciwę AB. Długość łuku AB jest równa π cm. Wyznacz miarę kąta zawartego między cięciwą AB a styczną do okręgu poprowadzoną w punkcie B. z czy to sie je?

kk: ∞π→→

ICSP: 3 lata

kk: o jest tu ktos, powiesz mi skad to:

	a+b
|AC|=		= c
	2

ICSP:

	a+b
|AE| =		= c
	2